КРОТОВАЯ НОРА
Крото́вая нора́, или «крото́вина», «кротови́на», а также «червячный переход» или «червото́чина» (последнее является дословным переводом англ. wormhole) — топологическая особенность пространства-времени, представляющая собой в каждый момент времени «тоннель» в пространстве. Эти области могут быть как связаны и помимо кротовой норы, представляя собой области единого пространства (см. пример на рисунке ниже), так и полностью разъединены, представляя собой отдельные пространства, связанные между собой только посредством кротовой норы.
Кротовые норы согласуются с общей теорией относительности. Понятие кротовой норы, включая её название (wormhole), ввёл в оборот американский физик Джон Арчибальд Уилер.
Для упрощённого представления о кротовой норе пространство представляется как двумерная (2D) поверхность. В этом случае кротовая нора будет выглядеть как отверстие в этой поверхности, переходящее в трёхмерную трубу (внутреннюю поверхность цилиндра), а затем вновь появляться в другом месте на двухмерной поверхности с отверстием, похожим на вход. Отличие реальной кротовой норы заключалось бы в числе пространственных измерений, которых было бы три. Например, вместо круглых входных и выходных отверстий в 2D-плоскости были бы сферы в 3D-пространстве.
Другой способ представить себе кротовые норы — взять лист бумаги и нарисовать две отдалённые точки на одной стороне листа. Лист бумаги представляет плоскость в пространственно-временном континууме, а две точки представляют расстояние, которое необходимо пройти. Однако теоретически кротовая нора может соединить эти две точки, если сложить эту плоскость так, чтобы точки касались друг друга. Поскольку две точки теперь соприкасаются, то пересечь расстояние будет намного легче.
Общая теория относительности (ОТО) допускает существование таких туннелей, хотя для существования проходимой кротовой норы необходимо, чтобы она была заполнена экзотической материей с отрицательной плотностью энергии[2], создающей сильное гравитационное отталкивание и препятствующей схлопыванию норы. Решения типа кротовых нор возникают в различных вариантах квантовой гравитации, хотя до полного исследования вопроса ещё очень далеко.
Область вблизи самого узкого участка кротовой норы называется «горловиной». Кротовые норы делятся на «внутримировые» (англ. intra-universe) и «межмировые» (англ. inter-universe), в зависимости от того, можно ли соединить её входы кривой, не пересекающей горловину.
Различают также проходимые (англ. traversable) и непроходимые кротовины. К последним относятся те туннели, которые коллапсируют слишком быстро для того, чтобы наблюдатель или сигнал (имеющие скорость не выше световой) успели добраться от одного входа до другого. Классический пример непроходимой кротовины — мост Эйнштейна — Розена в максимально расширенном пространстве Шварцшильда, а проходимой — кротовины Морриса — Торна.
Проходимая внутримировая кротовая нора даёт гипотетическую возможность путешествий во времени[3], если, например, один из её входов движется относительно другого, или если он находится в сильном гравитационном поле, где течение времени замедляется. Также кротовые норы гипотетически могут создавать возможность для межзвёздных путешествий, и в этом качестве кротовины нередко встречаются в научной фантастике.
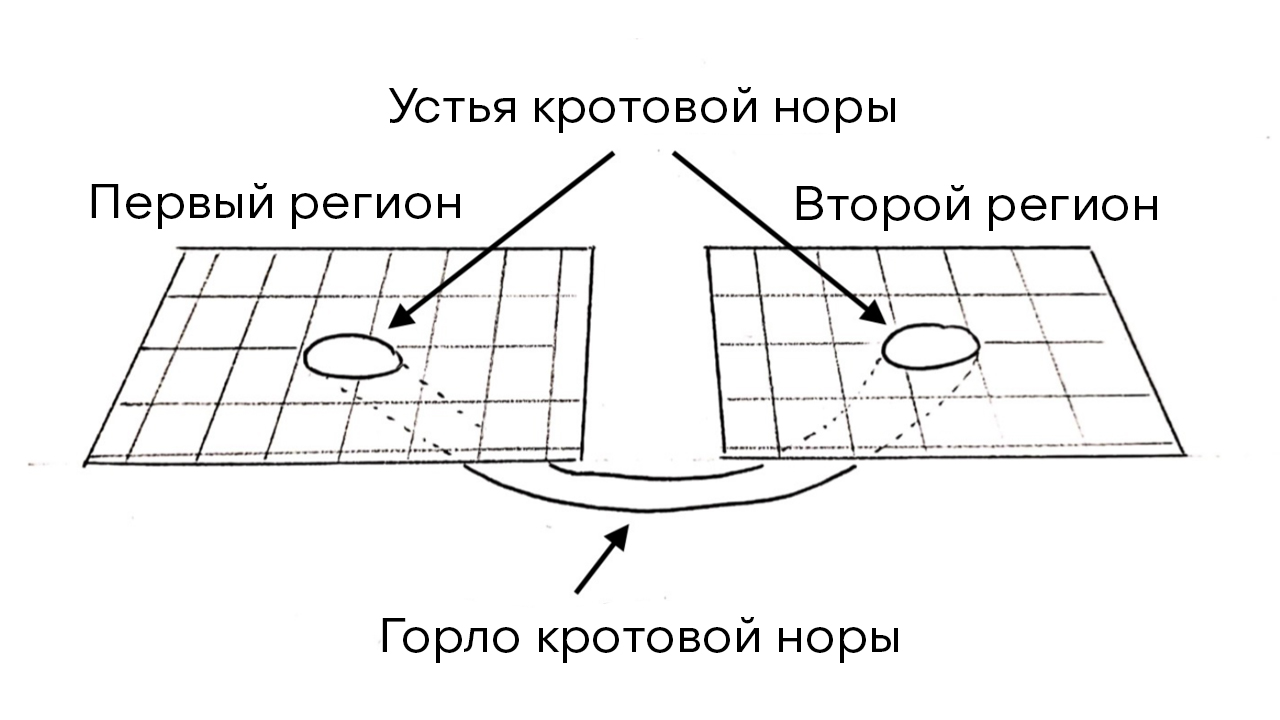
Червоточины, кротовины или кротовые норы (англ.: Wormholes) — это гипотетические пространственно-временные структуры с нетривиальной топологией (см. примечание 1), соединяющие либо две области одной вселенной, либо две разные вселенные (см. рис. 1). Входы в червоточину называются «устьями», а область между «устьями» (mouth) именуют «горлом» (throat). Простейшая конфигурация кротовой норы представляет собой два устья, соединенных одним горлом. Возможны и более сложные структуры кротовин [1].
Примечание переводчика 1: Тривиальной топологией называют ту топологию, которая обладает минимальным возможным количеством открытых множеств, т.е. пустого множества и всего пространства. Если предположить, что существуют две разных вселенные, обладающие топологией сферы и соединяющиеся между собой только одной кротовой норой, то такое пространство-время будет обладать тривиальной топологией сферы. Если же кротовиной соединяются между собой две разные части одной вселенной, то такое пространство-время будет обладать уже нетривиальной топологией тора. Если две вселенные, обладающие топологией сферы, соединяются между собой двумя и более кротовыми норами, то результирующее пространство-время также будет обладать нетривиальной топологией. Система вселенных, соединенных между собой несколькими кротовыми норами, также будет обладать нетривиальной топологией.
Червоточины не являются предсказанием ни одной теории гравитации, в т.ч. ОТО, и об их существовании можно делать лишь предположения, основанные на том, что кротовые норы представляют собой пространственно-временные структуры, существование которых вероятно в искривленных пространствах. Механизм образования и существования этих структур описывается в зависимости от конкретной теории гравитации по-разному — отсюда и исходят проблемы существования червоточин в нашей Вселенной.
Первые попытки решить проблему кротовых нор относят к Эйнштейну и Розену (см. раздел «Формирование…»), [2], а сами червоточины впервые были рассмотрены Мизнером и Уилером в 1957 году [3]. Существуют так называемые «проходимые» и «непроходимые» кротовины и особый интерес к себе привлекают именно проходимые — это те, которые можно пересекать в обоих направлениях, т.е. те, которые являются коротким путем для путешествий на большие расстояния без нарушения скоростного предела. В ОТО проходимые червоточины допустимы лишь при наличии экзотического вида материи, чтобы устья кротовых нор постоянно были открыты — в противном случае червоточина будет схлопываться и закрывать свои устья [6-8], вероятно, превращаясь в обычную черную дыру. В других теориях гравитации надобности в экзотической материи нет [11-14].
Поскольку мы не можем быть уверены в абсолютной правильности теории относительности для нашей Вселенной, то можем предполагать, что проходимые червоточины могут существовать и без специального вида материи. Астрофизические наблюдения могут искать кротовые норы, и за последние тридцать лет сформировалось несколько гипотез их поиска во Вселенной, которые стали особенно актуальны в последние годы, связанные со стремительным прогрессом средств наблюдений, способствующих изучению и поиску новых методов наблюдений кротовин.
В данном материале будут рассмотрены основные методы поиска макроскопических проходимых червоточин. Сначала будут описаны основные механизмы формирования и стабильности проходимых кротовых нор, затем будут рассмотрены сами методы их поиска и наши успехи, связанные с этими методами.

